Signature 签名

Signing is used when integrity is important. It is meant to be a guarantee that data sent from A to B was not altered.

So A signs the data by calculating the hash of the data and encrypting that hash using an asymmetric private key. B can then verify the data by calculating the hash of the data and decrypting the signature to compare if both hashes are the same.

A对data进行哈希之后，使用非对称加密的私钥对哈希值进行加密，生成签名。B对data哈希之后，使用公钥对A生成的签名进行解密，得到A对data的哈希值，验证这两个哈希值是否相等。

RAW signatures

A raw signature is usually calculated as follows:

create a hash of the data (e.g. SHA-256 hash)

encrypt the hash using an asymmetric private key (e.g. RSA 2048 bit key)

(optionally) encode the binary encrypted hash using base64 encoding

B will have to get the certificate with the public key as well. This might have been exchanged before. So at least 3 files are involved: the data, the signature and the certificate.

CMS signatures

A CMS signature is a standardized way to send data + signature + certificate with the public key all in one file from A to B. As long as the certificate is valid and not revoked, B can use the supplied public key to verify the signature.

SOAP signatures

A SOAP signature also contains data and the signature and optionally the certificate. All in one XML payload. There are special steps involved in calculating the hash of the data. This has to do with the fact that the SOAP XML sent from system to system might introduce extra elements or timestamps. Also, SOAP Signing offers the possibility to sign different parts of the message by different parties.

Email signatures

Sending emails is not very difficult. You have to fill in some data and send it to a server that forwards it, and eventually it will end up at its destination. However, it is possible to send emails with a FROM field that is not your own email address. In order to guarantee to your receiver that you really sent this email, you can sign your email. A trusted third party will check your identity and issue an email signing certificate. You install the private key in your email application and configure it to sign emails that you send out. The certificate is issued on a specific email address and all others that receive this email will see an indication that the sender is verified, because their tools will verify the signature using the public certificate that was issued by the trusted third party.

PDF or Word or other signatures

Adobe PDF documents and Microsoft Word documents are also examples of things that support signing. The signature is also inside the same document as the data so there is some description on what is part of the data and what is part of the metadata. Governments usually send official documents with a PDF that contains a certificate.

RSA加密、解密、签名、验签

这里将A理解为客户端，B理解为服务端，A、B分别有一对公钥和私钥。

加解密过程简述
A和B进行通信加密,B要先生成一对RSA密钥,B自己持有私钥,给A公钥 —>A使用B的公钥加密要发送的内容,然后B接收到密文后通过自己的私钥解密内容

签名验签过程简述
A给B发送消息,A先计算出消息的消息摘要,然后使用自己的私钥加密消息摘要,被加密的消息摘要就是签名.(A用自己的私钥给消息摘要加密成为签名)
B收到消息后,也会使用和A相同的方法提取消息摘要,然后用A的公钥解密签名,并与自己计算出来的消息摘要进行比较–>如果相同则说明消息是A发送给B的,同时,A也无法否认自己发送消息给B的事实.(B使用A的公钥解密签名文件的过程,叫做"验签").

签名过程:

A计算消息m的消息摘要,记为 h(m)
A使用私钥(n,d)对h(m)加密,生成签名s, s满足:s=(h(m))^d mod n;
由于A是用自己的私钥对消息摘要加密,所以只用使用s的公钥才能解密该消息摘要,这样A就不可否认自己发送了该消息给B.
A发送消息和签名(m,s)给B

验签过程:

B计算消息m的消息摘要(计算方式和A相同),记为h(m)
B使用A的公钥(n,e)解密s,得到 H(m), H(m) = s^e mod n
B比较H(m)与h(m),相同才能证明验签成功

RSA

Assignment

Now suppose you have the following private key:

1
2
3

Then what was the modulus of the public key and now provide a signature for us based on that modulus .

题目给出了一个rsa私钥，要求找出它的模，并对模签名。

使用openssl工具可以实现：

查看openssl手册：

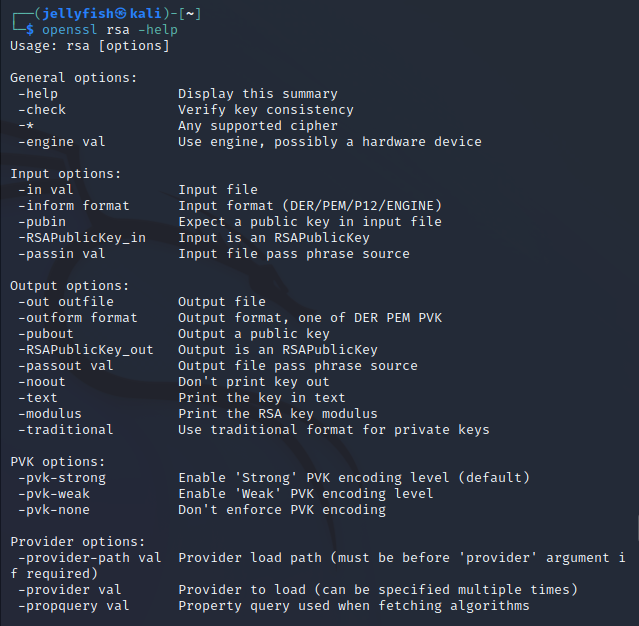
把题目中给出的私钥存起来放在文件private.key中，使用-modulus可以算出模：

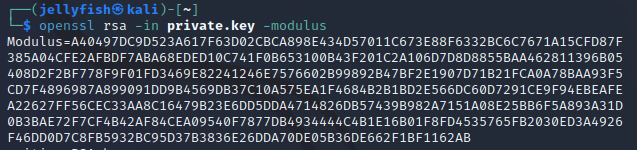
查看openssl dgst的手册，可以找到一些签名方法：

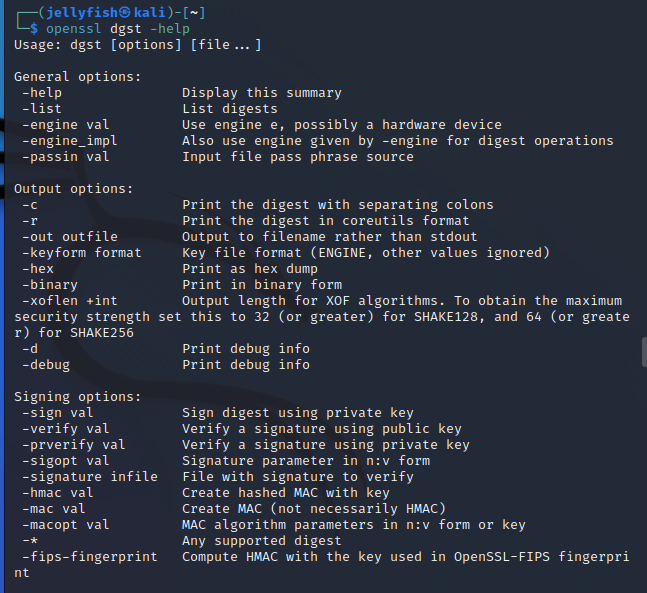
-sign val ：使用私钥对消息进行签名：（使用sha256进行哈希）

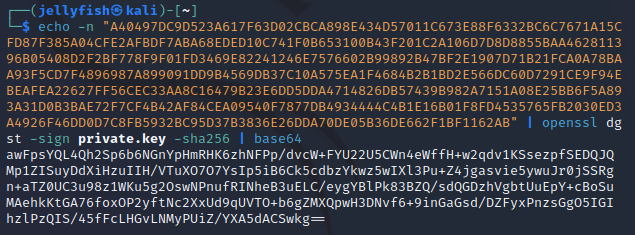
于是生成了签名。