散列函数与认证

一、简介

认证：
防止主动攻击，如伪装、篡改、干扰
实体认证：
验证发送者是真的，不是冒充的。
消息认证：
验证消息的完整性，没有被篡改、重放、延迟。
认证系统的组成：
认证编码器
认证译码器
认证系统的工作原理：
发送方使用认证函数来产生一个认证标识，接收方使用认证协议，基于验证标识验证真实性。
认证函数的分类：
1.加密函数：用整个消息的密文作为消息认证的认证标识；（例如cbc）
2.消息认证码(MAC)：指消息被一密钥控制的公开函数作用后产生的、用作认证符的、固定长度的数值，也称为密码校验和；
3.散列函数：一个不需要密钥的公开函数，将任意长度的输入消息映射成一个固定长度的输出值，并以此值作为认证标识别。
认证系统的基本设计标准：
特定的接收者能够检验和证实消息的合法性、真实性和完整性；
消息的发送者和接收者不能抵赖；
除了合法的消息发送者，其它人不能伪造合法的消息。

备注：
1.消息记作m，认证标识记作$C_{m}$，通常长度上来说$C_{m}< m$ 。用$C_{m}$校验$m$的完整性，$C_{m}$要继承m所有的特征属性。
2.固定长度的隐患：
把一个不固定长度的输入映射到一个固定长度的空间，前者是个很大的空间，后者相比之下是个极小的空间。有可能使得有两个密文对应同一个消息验证码。如果攻击者把消息替换了，但验证码还是不变，失去了验证功能。
此为“碰撞”。需要仔细设计认证函数，使得碰撞很难。

二、基于消息加密的认证

1.对称加密体制实现加密和认证

基于密钥的保密性，在加密时可以提供认证。
不足在于：
1.不能数字签名。接收方可伪造，发送方可否认，因为无法证明消息确实是由特定发送方发送的，理论上任何拥有密钥的人都可以生成相同的消息。
2.需要额外的差错检验来确保消息的完整性。例如分组加密的CBC模式，最后一个密文块确实与整个消息的内容有关，但它本身并不提供消息的真实性或完整性保证。如果攻击者篡改了密文中的某一块，这种改变会在解密时传播，导致特定块的明文发生变化，这不足以作为有效的“验证标识”来确认消息的完整性和真实性。

2.非对称加密体制实现加密和认证

非对称密码体制可以用来加密、认证、签名。
在发送者用自己的私钥签名以后，用接收者的公钥进行加密。接收者用自己的私钥解密消息后，用发送者的公钥验证签名。（注：这是两套不同的密钥。）
不足之处在于双方都要进行两次密码变换，开销比较大。

三、消息认证码

指消息被一密钥控制的公开函数作用后产生的、用作认证符的、固定长度的数值，也称为密码校验和。
工作原理：
明文记作m。
A首先计算$MAC = C_k(m)$，其中$C_k(·)$是密钥控制的公开函数，然后向B发送$m || MAC$；(m串接MAC)
B收到后做与A相同的计算，求得一新MAC，并与收到的MAC做比较。
如果两者相等，就认为报文没有被篡改，并相信报文来自声称的发送者。如果两者不等，认证不通过。
不足：
1.无数字签名，因为认证编码密钥和解码密钥相同。
2.不提供消息的机密性，因为MAC函数无需可逆，不能用MAC来加密。
改进： 实现加密机制。
1.与明文相关
$E_{k2}(m || C_{k1}(m))$ 把整个报文加密.
加密的长度更大，计算开销更大，安全性相对较好。
2.与密文相关
$E_{k2}(m) || C_{k1}(E_{k2}(m))$ 把明文加密，计算密文的验证码，两者串接起来。

四、散列函数

hash函数是一个单向函数，把消息映射为固定长度的结果，是不可逆的，不需要用认证码还原消息。

1.设计目标：

1.函数的输入$x$是任意长；
2.函数的输出$H(x)$是固定长；
3.已知$x$，求$H(x)$较为容易，可以用硬件或软件实现；
(前三条是Hash函数用于消息验证的基本要求。)
4.已知$h$，求使得$H(x) = h$的$x$在计算上是不可行的；
(用于带秘密值得认证，如$c=H(s||m)$，如果已知$c$就能求出$s||m$,则秘密值泄露。)
5.已知$x$，找出$y(y≠x)$使得$H(x) = H(y)$在计算上是不可行的;
(弱单向性：用于防止消息被伪造。发送方发送的消息$x$被伪造成$y$了。)
6.找出任意两个不同的输入$x,y$，使得$H(x) = H(y)$在计算上是不可行的。
(强单向性：用于抵抗生日攻击。)

2.生日攻击：

(哈希函数H有n个可能的输出，输出为m比特长)

第I类生日攻击

H(x)是一个特定的输出，如果对H随机取k个输入，则至少有一个输入y使得H(y) = H(x)的概率为0.5时，k有多大？

第II类生日攻击

如果对H随机取k个输入，则至少有两个输入产生相同输出的概率大于0.5，k应该有多大？

3.迭代型Hash函数

介绍

MD5：产生128位的信息摘要。
MD5以512位分组来处理输入文本，输入$M$分为$L$个分组$Y_0, Y_1, …, Y_{L-1}$.每个分组512 bit。每一分组又划分为16个32位子分组，这就是16个字。（一个字四字节，4Byte=32bit）。算法的输出由四个32位分组组成，将它们级联形成一个128位散列值。

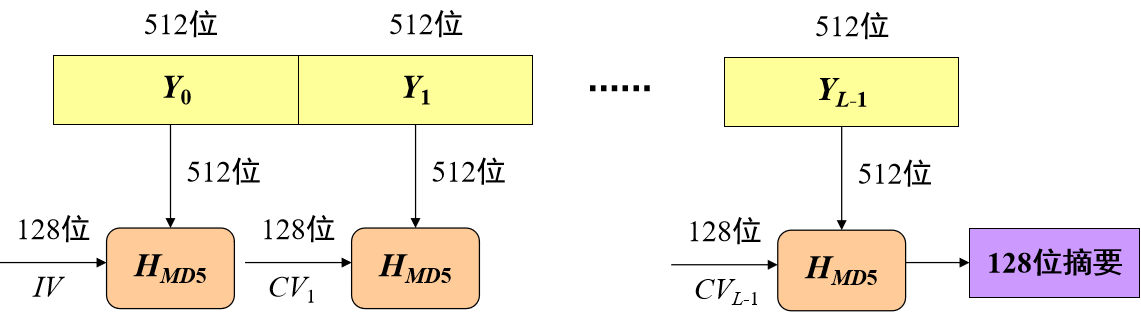
每次$H_{MD5}$ 把一个分组$Y$由512位压缩到128位，再和缓冲区中的$CV_{i}$或者$IV$相加，得到输出。最后一次的输出作为消息摘要值。$H(M) = CV_{L}$

每次$H_{MD5}$ 有四轮处理，每一轮处理有16次迭代，所以每次压缩需要64次迭代。

MD5算法组成

填充
附加消息的长度
对MD缓冲区初始化
以分组为单位对消息进行处理

1.填充

使得消息比特长在模512下为448，即填充后消息的长度为512的某一倍数减64。(这64位用于表示消息长度。)
填充时，首先在消息末端附一个“1” ，然后再后接所需要的多个“0”。
当消息的长度为512的整数倍时，仍需要填充一个完整的分组，用于统一接口。

2.附加消息的长度

填充后消息的尾部的64位用来表示未填充时消息的长度，以little-endian方式来表示。所以MD5能处理的消息长度最大$2^{64}$it。尽管它能处理的消息长度有限，但在实际应用中已经足够了。
这样的处理使得该填充方案是可逆的，可以找到原始的消息。分组处理常常采用可逆的填充方案。

3.对MD缓冲区初始化

缓冲区可以表示为4个32位的寄存器(A, B, C, D)
$IV$(或$CV_{0}$（初始向量）：
A = 0x01234567
B = 0x89abcdef
C = 0xfedcba98
D = 0x76543210

4.以分组为单位对消息进行处理

在每一轮的16次迭代中，每次迭代的过程如下图所示。

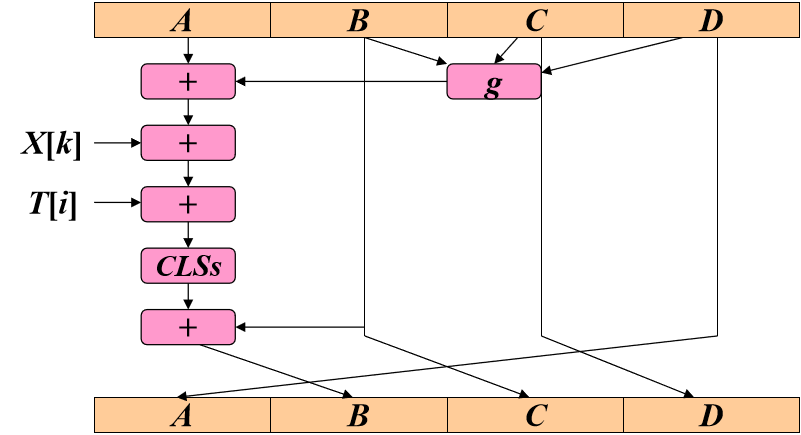
ABCD:
缓冲区的寄存器，其中A,C,D来自上一轮的D,B,C。B来自上一轮A参与运算后的结果.
X[k]：
分组内的第k个子分组。一个分组512位，被划分成了16个32位的子分组。（每一迭代运算32位，所以需要迭代16次，共512位。)
CLSs：
循环左移s位
T[i]:
T是一个常数表，有64个元素，一个元素对应一次迭代。四轮处理，每轮16次迭代，所以常数表中需要64个元素。
常数表有64个元素，第i个元素$T[i]$为$2^{32}×abs(sin(i))$的整数部分。
sin为正弦函数；i以弧度为单位；abs为取绝对值。
将T划分为T[1,…,16], T[17,…,32], T[33,…,48], T[49,…,64]。
+:
模$2^{32}$加法。
g：
逻辑函数。每一轮使用一个逻辑函数。四轮的逻辑函数分别为F,G,H,I。

轮数	基本逻辑函数	g(b,c,d)
1	F(b,c,d)	(b∧c) ∨(~b∧d)
2	G(b,c,d)	(b∧d) ∨(c∧~d)
3	H(b,c,d)	b⊕c⊕d
4	I(b,c,d)	c⊕(b∨~d)

轮处理：
四轮处理过程中，每轮以不同的次序使用16个字。
第一轮以字的初始次序使用；第二轮到第四轮，分别对字的次序i做置换后得到一个新的次序，然后使用新次序使用16个字。
第二到第四轮三个置换分别为
$v2(i) = (1 + 5i) mod 16$
$v3(i) = (1 + 5i) mod 16$
$v4(i) = (1 + 5i) mod 16$

五、SHA-1

SHA是美国NIST和NSA共同设计的安全散列算法(Secure Hash Algorithm)，用于数字签名标准DSS(Digital Signature Standard)。

SHA-1的值域空间
输入：长度小于$2^{64}$位的消息
输出：160位的消息摘要。

使用时如果消息超出长度限制，则取模。
比MD5改进之处在于输出空间变大，碰撞概率降低。

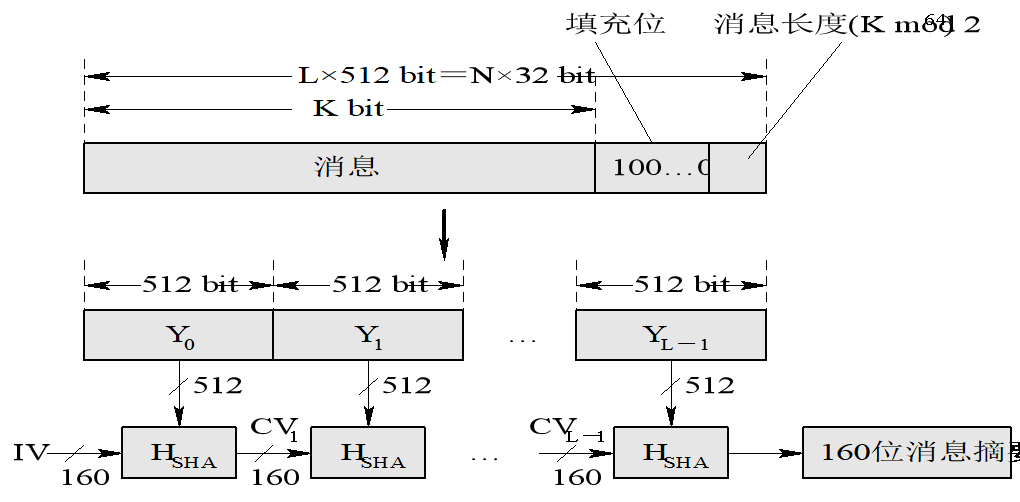
注：图中消息长度为$k (mod 2^{64})$

算法和MD5一样也分为四个部分：
填充
附加消息的长度
对缓冲区初始化
160位的缓冲区，则使用五个32位的寄存器A、B、C、D、E。
A = 0x67452301
B = 0xEFCDAB89
C = 0x98BADCFE
D = 0x10325476
E = 0xC3D2E1F0
以分组为单位对消息进行处理

SHA运算主循环包括四轮，每轮20次操作
每一步迭代运算的运算形式

$$A' = (E + f_{t}(B, C, D) + CLS_{5}(A) + W_{t} + K_{t})$$

$$B = A$$

$$C = CLS_{30}(B)$$

$$D = C$$

$$E = D$$

每个循环还使用一个额外的常数值$K_{t}$。$\{K_{0}、K_{1}、…、K_{79}\}$
$K_{t} = 0x5A827999 (0≤t≤19)$
$K_{t} = 0x6ED9EBA1 (20≤t≤39)$
$K_{t} = 0x8F1BBCDC (40≤t≤59)$
$K_{t} = 0xCA62C1D6 (60≤t≤79)$

基本逻辑函数——$f_{t}$
$f_{t}(B,C,D) = (B\land C)\lor (\bar{B} \land D) (0≤t≤19)$
$f_{t}(B,C,D) = B＋C＋D (20≤t≤39)$
f_{t}(B,C,D) = (B\land C)\or (B\and D)\or (C\and D) (40≤t≤59)
$f_{t}(B,C,D) = B＋C＋D (60≤t≤79)$

第二个和第四个逻辑函数是一样的。而MD5的逻辑函数是不一样的。

$W_{t}$ ——由当前512比特长的分组导出的一个32比特的字
前16个值$(W_{0},…, W_{15})$直接取输入分组的16个相应的字
其余$(W_{16} ,…, W_{79})$取为： $W_{t} = CLS_{1}(W_{t-16} + W_{t-14} + W_{t-8} + W_{t-3})$
$CLS_{t}$——循环左移动 “t” 位
$“+”$——模$2^{32}$加法

六、SHA-1与MD5比较

MD5是对MD4的改进。
SHA–1是在MD4的基础上开发的，结构非常类似。

	SHA-1	MD5
HASH值长度	160bit	128bit
分组处理长度	512bit	512bit
操作步数	80(4×20)	64(4×16)
最大消息长	≤$2^{64}$ bit	不限
非线形函数	3(第2、4轮相同)	4
常数个数	4	64