一、安全协议的安全性质

1.机密性（加解密）
2.完整性（哈希）
3.认证性（签名）
4.不可否认性（签名）
5.公平性（分蛋糕）

二、对安全协议的攻击

1.重放/预重放攻击

重放：攻击者把之前运行协议中的消息或部分消息插入到当前运行的协议。
**预重放：**重放攻击的一种扩展攻击 。
eg:
转账：A给银行发送数据包，要求给B转100元。拦截该数据包重放多次，B收到很多钱。

解决办法：打时间戳，设置有效时间。

预重放：
1.敌手Malice首先窃听Alice和Bob的通信（得到部分秘密）；
2.Malice用真实的身份分别与Alice和Bob通信；
3.Malice利用“1”中的部分信息诱使Alice和Bob透露部分秘密信息（根据信息的logic，可能通过合法身份套取一部分秘密信息。）；
4.Malice利用得到的秘密信息计算出Alice和Bob通信的密钥。

2.反射攻击

典型情形：
相同协议的并行运行——并行会话攻击
实例
Alice和Bob通过表明知道共享的密钥K来达到相互认证
 Alice −> Bob: {NA}K Bob->Alice: {NB}K,NA Alice −> Bob: NB\begin{array}{l}\text { Alice }->\text { Bob: }\left\{N_{A}\right\}_{K} \\ \text { Bob->Alice: }\left\{N_{B}\right\}_{K}, N_{A} \\ \text { Alice }->\text { Bob: } N_{B}\end{array}

反射：

 1.Alice->Malice: {NA}K 2.Malice-> Alice: {NA}K 2.Alice->Malice: {NA′}K,NA 1.Malice-> Alice: {NA′}K,NA 1.Alice->Malice: NA′ 2.Malice->Alice NA′\begin{array}{l}\text { 1.Alice->Malice: }\left\{N_{A}\right\}_{K} \\ \text { 2.Malice-> Alice: }\left\{N_{A}\right\}_{K} \\ \text { 2.Alice->Malice: }\left\{N_{A}^{\prime}\right\}_{K}, N_{A} \\ \text { 1.Malice-> Alice: }\left\{N_{A}^{\prime}\right\}_{K}, N_{A} \\ \text { 1.Alice->Malice: } N_{A}^{\prime} \\ \text { 2.Malice->Alice } N_{A}^{\prime}\end{array}

3.类型攻击

当用户接收到的信息都是二进制串时，用户无法判断是否是加密传输，用户可能会将一个消息错误的解释成其它不同类型的的消息。本来为实体的标识符可能被错误的解释成一个密钥。
实例：对Otway和Rees协议的类型攻击
协议描述
Alice和Bob分别与Server共享一个长期密钥KAS和KBS
Server生成新的会话密钥KAB并传递给Alice和Bob

1.Alice->Bob:M,Alice,Bob, {NA,M,Alice,Bob}KAS\left\{N_{A}, M\right., Alice,\left.B o b\right\} \boldsymbol{K}_{A S}
2.Bob->Server: M,Alice,Bob,{NA,M,Alice,Bob}KAS,{NB,M,Alice,Bob}KBSM, Alice, Bob ,\left\{N_{A}, M\right., Alice,\left.B o b\right\} K_{A S},\left\{N_{B}, M\right., Alice,\left.B o b\right\} K_{B S}
3.Server −>-> Bob: M,{NA,KAB}KAS,{NB,KAB}KBSM,\left\{N_{A}, K_{A B}\right\} K_{A S},\left\{N_{B}, K_{A B}\right\} K_{B S}
4.Bob -> Alice: M,{NA,KAB}KASM,\left\{N_{A}, K_{A B}\right\} \boldsymbol{K}_{A S} (Alice 要验证 NaN a, 才会相信。)

第一步中发送的{NA,M,Alice,Bob}KAS\{N_A,M,Alice,Bob\}K_{AS}和第四步中发送的{NA,KAB}KAS\{N_A,K_{AB}\}K_{AS}的结构是相同的。于是Alice把{M,Alice,Bob}\{M,Alice,Bob\}当作KABK_{AB}。
防范方法：结构不要同构。

4.证书操纵攻击

攻击：(左：无身份验证。右：攻击。)
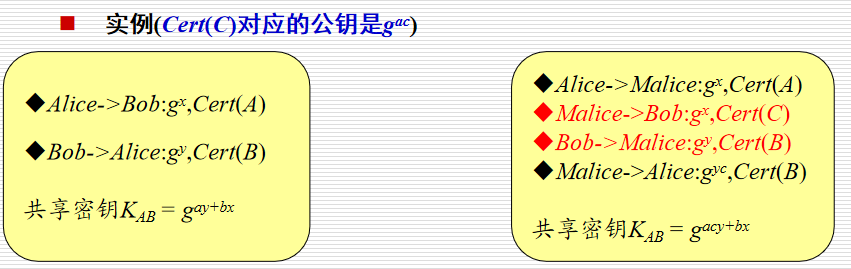
image-20240511151138103

共享密钥KAB=gacy+bxK_{AB} = g^{acy+bx}
bob相信了alice的证书是Cert©

5.协议攻击者模型——Dolev和Yao(姚期智)模型

可以窃听所有经过网络的消息
可以阻止和截获所有经过网络的消息
可以存储所获得或自身创造的消息
可以根据存储的消息伪造消息，并发送该消息
可以作为合法的主体参与协议的运行

三、基本的安全协议

1.秘密分割

把一个消息分成n块，单独的每一块看起来没有意义，但所有的块集合起来能恢复出消息。

在可信第三方Trent的主导下将某秘密进行分割在Alice与Bob之间共享的简单协议

秘密分割：
Trent产生一随机比特R(R和M一样长度)
Trent用R异或M得到S = R⊕M
Trent将R给Alice，将S给Bob
秘密重构：
Alice和Bob将他们的消息异或就可以得到消息M = R⊕ S

基于主密钥的信息安全系统的缺陷
主密钥偶然或有意地被泄露，系统中的秘密信息会遭受攻击
主密钥丢失或损坏，系统中的秘密信息将无法恢复
主密钥的解决方案导致权力过于集中——密钥管理

2.秘密共享

每人都带一些冗余。

门限方案：实现门限访问结构的秘密共享
一个(m,n)的门限访问结构
m为门限值
秘密SK被拆分为n个份额的共享秘密
利用任意m个或更多个共享份额可以恢复秘密SK
任何m-1或更少的共享份额是不能得到关于秘密SK的任何有用信息

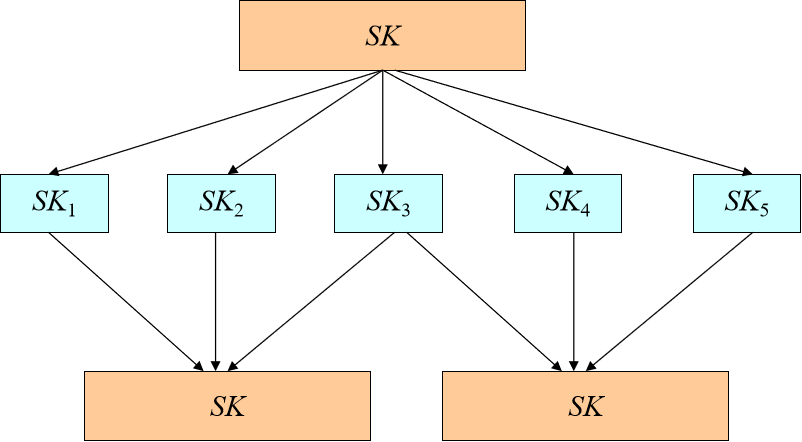
image-20240416104053039

(3,5)门限秘密共享方案
Shamir 门限方案｜秘密共享｜拉格朗日插值｜密码学_shamir门限方案-CSDN博客

五个方程，三个变量，系数矩阵的秩为3。

基于拉格朗日插值多项式的秘密共享(m,n)门限方案（算法细节，小班课）
函数拟合：构造f1f_{1}逼近f2f_{2}
（m,n)门限
f(x)=S+a1x1+a2x2+...+ak−1xk−1f(x)=S+a_1x_1+a_2x_2+...+a_{k−1}x_{k−1}

每个人拿到（p,xi,f(xi）)。解m元一次方程组。
系数矩阵的秩=m.才能求出唯一解。
xi!=xj。所以系数矩阵的秩=m,可以求出。

3.阈下信道

通过无害签名，建立阈下信道实现秘密信息交换。

本质是数字签名
阈下信道签名算法与普通的签名算法不能区别
阈下信道的基本过程
Alice随机产生一个无害消息
Alice对这个无害信息签名，她在签名中隐藏阈下信息
Alice通过Walter发送签名消息给Bob
Walter读这份无害的信息并检查签名，并转发给Bob
Bob检查这份无害消息的签名，并确认来自Alice
Bob忽略无害的消息，提取阈下信息

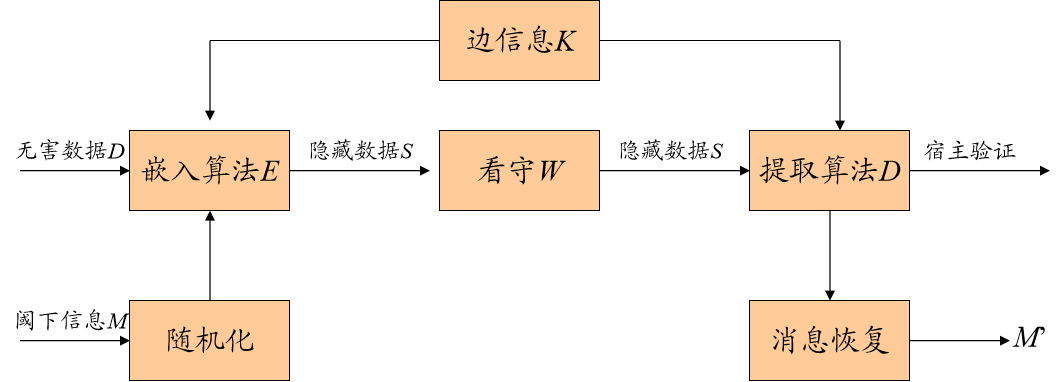
image-20240416110034164

RSA数字签名HASH阈下信道
处理流程
签名者取两个随机大素数p和q（保密），计算公开的模数r=pq(公开)，计算秘密的欧拉函数ϕ(r)=（p−1）(q−1)\phi (r) =（p-1）(q-1)（保密）。
随机选取整数e，满足gcd(e,ϕ(r))=1gcd(e, \phi(r))=1(公开e，验证密钥)
计算d，满足de≡1(modϕ(r))de≡1(mod \phi (r))(签名密钥)
签名：y=H(x)d(modr)y=H(x)^d(mod r), 把x||y发送给验证者
验证：检查下式是否成立yd=H(x)(modr)yd=H(x) (mod r).

选择x的不同表达方式，使得H(x)中的某些位为阈下信息

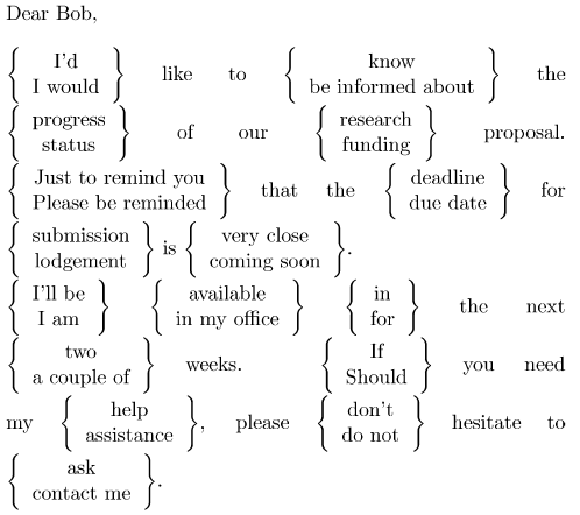
image-20240416110308005

4.比特承诺

承诺方案
Alice想对Bob承诺一个预测（即1bit或bit序列），但直到某个时间以后才揭示她的预测。而另一方面，Bob想确信在Alice承诺了她的预测后，她没有改变她的想法。

基本过程
承诺者Alice向接收者Bob承诺一个消息，承诺过程要求，Alice向Bob承诺时，Bob不可能获得关于被承诺消息的任何信息；
经过一段时间后，Alice能够向Bob证实她所承诺的消息，但是Alice无法欺骗Bob（操控加密密钥使得加密后的消息发生改变）。

协议
Alice把消息m放在一个箱子里并锁住（只有Alice有钥匙可以打开箱子）送给Bob；
当Alice决定向Bob证实消息时，Alice会把消息m及钥匙给Bob；
钥匙是否可以操控m？

Bob能够打开箱子并验证箱子里的消息与Alice出示的消息相同，并且Bob确信箱子里的消息在他的保管期间没有被篡改。

构造比特承诺的两大元素
哈希函数
加密/签名

过程实例一
Alice承诺b（使用对称密码算法）
Bob产生一个随机比特串R，并把它发送给Alice。
Alice生成一个由她想承诺的比特b组成的消息（b实际上可能是几个比特），以及Bob的随机串。她用某个随机密钥k对它加密，并将结果Ek(R，b)送回给Bob。
Alice揭示b
当到了Alice揭示她的比特的时候，协议继续：
Alice发送密钥给Bob；
Bob解密消息以揭示比特。他检测他的随机串以证实比特的有效性。
b是用来防止alice利用对称密钥来控制并改变消息，因为很难找到一个密钥刚好改变前几位而不改变后几位。
比特承诺：可以只承诺一位。如果只承诺一位，有很大机会通过某一特定密钥计算这一位使得这一位一定是0/1。

过程实例二
Alice承诺b（使用单向函数的比特承诺）
Alice产生两个随机比特串，R1和R2
Alice产生消息，该消息由她的随机串和她希望承诺的比特组成(R1，R2，b)
Alice计算消息的单向函数值，将结果以及其中一个随机串发送给Bob。H(R1，R2，b)|R1
当到了Alice揭示她的比特的时候，协议继续
Alice将原消息发给Bob。(R1，R2，b)
Bob计算消息的单向函数值，并将该值及R1与原先第3步收到的值及随机串比较。如匹配，则比特有效

这个协议中bob没有参与任何参数的选择。
可以看作一个R，拆分为R1,R2。
只选一个R，有什么问题？
R很长，b只有几位，bob可以穷举来计算hash值，从而猜出b。
为了降低bob猜出b而进行欺骗的概率，通常R1长度等于R2长度。

过程实例三
Alice承诺（使用伪随机序列发生器的比特承诺）
1.Bob产生随机比特串RB，并送给Alice
2.Alice为伪随机比特发生器生成一个随机种子。然后，对Bob随机比特串中的每一比特，她回送Bob下面两个中的一个：(a)如果Bob比特为0，发生器输出比特值；(b)如果Bob的比特为1，发生器输出与她的承诺比特的异或
当到了Alice揭示她的比特的时候，协议继续
3.Alice将随机种子送给Bob
4.Bob完成第（2）步确认Alice的行动是合理的。
如果Bob的随机比特串足够长，伪随机比特发生器不可预测，这时Alice就无有效的方法进行欺诈。

模糊点：https://blog.csdn.net/simanstar/article/details/50965931

Alice送给Bob以便对比特承诺的这些串有时又叫模糊点。一个模糊点是一个比特序列，虽然在协议中没有说明它为什么必须这样，正如Gilles Brassard所说的，“只要是合理存在的就是有用的”[236]。模糊点有下面四个特性：
1.Alice能够对模糊点承诺，通过承诺模糊点来承诺一个比特。
2.Alice能够打开她所承诺的任何模糊点。当她打开模糊点时，她能让Bob相信在她对模糊点承诺时她所承诺的比特值。因此，她不能选择把任何模糊点作为0或1打开。
3.Bob不知道Alice如何打开承诺了的但尚未打开的模糊点。即使Alice打开别的模糊点之后，也是如此。
4.模糊点所带的信息除Alice承诺的比特外，不再有任何信息。模糊点本身，连同Alice承诺和开启模糊点的过程，与Alice希望对Bob保密的别的东西不相关。