安全多方计算
安全多方计算
**多方计算问题:**一组参与者希望共同计算某个约定的函数,函数的输入参数有多个,每个参与者提供函数的一个输入,除了函数的输出外,没有人知道关于任何其它成员输入的任何事情 。
一、密码学家晚餐问题
1.场景描述
三个密码学家(Alice Bob Carol)坐在他们最喜欢的三星级餐馆准备吃晚餐,侍者通知他们晚餐需匿名支付账单,其中一个密码学家可能正在付账,也可能这顿晚餐已由美国国家安全局NSA付账。三位密码学家彼此尊重匿名付账的权利,但又需要知道是不是NSA在付账。
如何确定谁在付账同时又保护付账者的匿名性?
2.David Chaum的密码学家晚餐问题
一个简单有效的解决方案:
1.每个密码学家将菜单放置于左边而互相隔离开来(菜单:对称加密算法,隔开左手边的人)
2.每个人只能看到自己和右边密码学家的结果
3.每个密码学家在他和右边密码学家之间抛掷一枚硬币
4.每个密码学家广播她能看到的两枚硬币是同一面还是不同的一面
5.如果有一个密码学家付账,则他说相反的结果
判定结果
桌上说“不同”的人数为奇数——某个密码学家在付账
桌上说“不同”的人数为偶数——NSA在付账
如果某个密码学家在付账,另两人不能精确定位到该密码学家
两个密码学家进行“晚餐问题”,他们会知道谁付的账,旁观者只知道其中某个人付账或者NSA付账,不能精确定位。
任意数量的密码学家进行“晚餐问题”,他们可以全部坐成一个圈并在他们中抛掷硬币。
密码学家人数变为n时,结果是否仍成立?参考:密码学家晚餐问题(n>2情况) - 20211108俞振阳 - 博客园 (cnblogs.com)
首先引入XOR观念便于理解和阐释:
硬币的结果只为0或1,密码学家给出的真结果:1⊕0=1,1⊕1=0,0⊕1=1与0⊕0=0
假结果:1⊕0=0,1⊕1=1,0⊕1=0与0⊕0=1
对于n枚硬币,设为1有p个,为0有q个,每个硬币的状态为ai(ai=0或1),每位学家给出的结果为xi。
若没有学家付款,则:
若有一位学家付款,且不妨假设他是第一位学家,则:
同时,易知对于一系列0、1逐位异或的结果为0,若1的个数为偶数,为1,若0的个数为奇数。
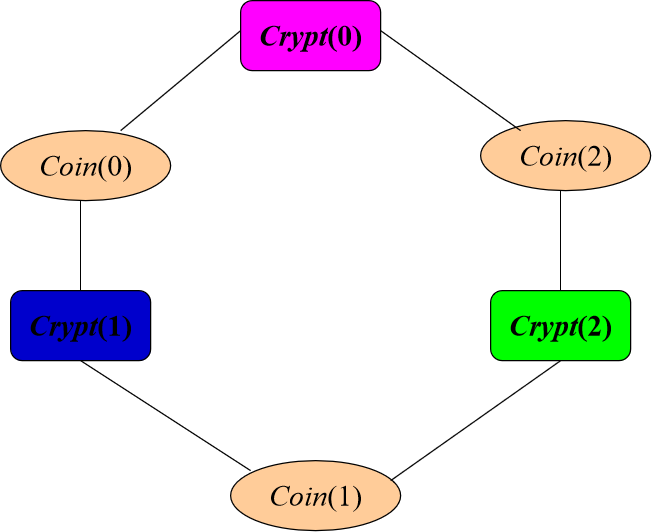
3.“晚餐问题”的应用——匿名消息广播
用户把他们自己排进一个逻辑圆圈,构造饭桌;
在一定的时间间隔内,相邻的每对用户对他们之间抛掷硬币;
使用一些公正的硬币抛掷协议防止窃听者;
在每次抛掷之后每个用户说“相同”或“不同”。
恶意的参与者不能读出报文,但他能通过在第三步撒谎来破坏系统。
二、平均工资问题
1.场景描述
Alice、Bob、Carol和Dave四人在一起工作,他们想了解四个人的平均工资。系统中无仲裁者,任何人都不想让其他人知道自己的工资。
2.解决方案
Alice生成一个随机数,将其与自己的工资相加,用Bob的公钥加密发送给Bob;
Bob用自己的私钥解密,加进自己的工资,然后用Carol的公钥加密发送给Carol;
Carol用自己的私钥解密,加进自己的工资,然后用Dave的公钥加密发送给Dave;
Dave用自己的私钥解密,加进自己的工资,然后用Alice的公钥加密发送给Alice;
Alice用自己的私钥解密,减去原来的随机数得到工资总和;
Alice将工资总和除以人数得到平均工资,宣布结果。
3.缺点
然而参与者可以谎报自己的结果,Alice也可以谎报最终的结果。
使用比特承诺可以解决“Alice谎报”缺陷:
运用比特承诺协议让Alice向Bob传送他的随机数,缺点在于协议结束后,Bob可以获知Alice的工资。
三、终身伴侣问题
1.场景描述
Alice、Bob都在相亲,出于隐私和含蓄,都不会给出自身条件和择偶标准。(假设自身条件和择偶标准可以写成固定格式的字符串,并且自身条件和择偶标注的字段名、顺序相同。)
如何匹配两人?
2.解决方案
使用一个单向函数,Alice将她的择偶要求m,HASH得到一个8位数字的字符串h(m)
Alice用这8位数字作为电话号码拨号,并留言;
Alice告诉Bob她为她的择偶要求申请一个单向函数的次数;
Bob用和Alice相同次数的HASH他的自身条件;
他也用这个8位数字作为电话号码,试图听取留言;
有留言,则配对成功。
3.缺点
Bob可以进行“选择明文攻击”:可以HASH普遍的择偶要求,拨打所得的电话号码,以窃听留言。
只有在不可能得到足够多的明文消息的情况下该协议安全。


