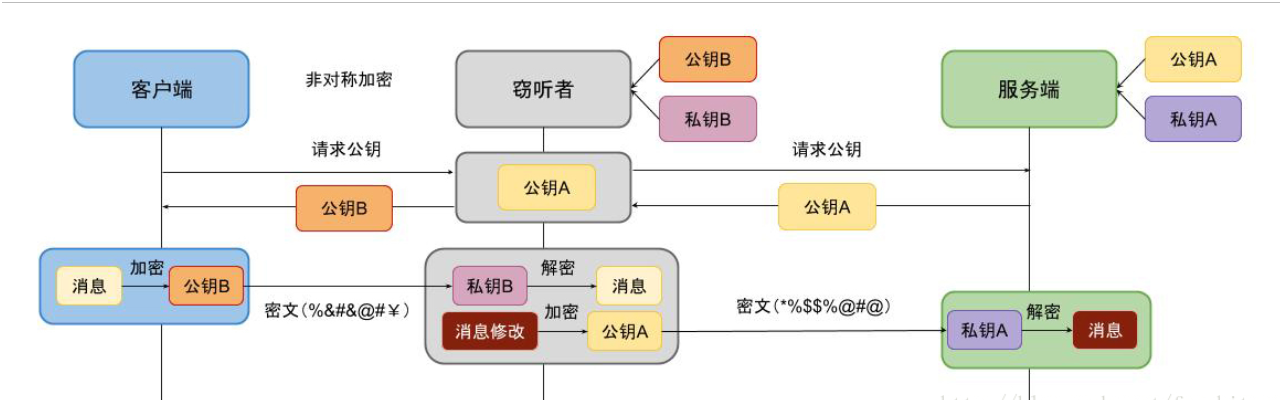
非对称加密体制

一、问题由来

加密通信中经常面临一个问题：陌生人之间加密通信需要如何管理和分发密钥？
对称密码体制在其中的困难有：
1.假设n个人通信，每人都要（n-1）个密钥，可信中心分发n(n−1)2\frac{n(n-1)}{2}个密钥。密钥太多难以管理。
2.陌生人不能提前约定密钥。
3.不能用作数字签名。

二、基础概念

密钥

(PK, SK)
PK：俗称公钥(Public Key)，通常公钥是公开的，可以被任何实体通过有效渠道获取；
SK：俗称私钥(Secret Key)，通常私钥是保密的，不能被任何实体通过非法渠道获取；
非对称加密通常基于数学函数而不是随机序列。

公钥和私钥之间具有一定关联。
公钥公开，用于加密，私钥解密，不能公开。
Alice在知道公钥和明文的情况下，容易计算，加密。
MIlice仅仅知道公钥而反推私钥，是困难的。
Milice知道公钥和密文，也很难解出明文。
Bob在拿到密文后，很容易根据私钥解密出明文。

加密函数

一个单向函数
一一映射的函数，才是可逆的：当x1≠x2x_{1} \ne x_{2}
一个可逆函数f：A→Bf：A\rightarrow B，若它满足：
对所有x∈Ax\in A，易于计算f(x)；
对“几乎所有x∈Ax\in A由f(x)求x“极为困难”，以至于实际上不可能做到，则称f为一单向(One-way)函数。

单项陷门函数

给定x，计算y = f(x)是容易的；
给定y，计算x使y = f(x)是困难的；
存在z，已知z时, 对给定的任何y，若相应的x存在，则计算x使y = f(x)是容易的。
陷门作为私钥

密码通信

密码通信分为两个不同阶段。
会话密钥交换阶段：用来协商接下来的密钥——对称加密的密钥。
保密信息交换阶段：流密码或分组密码。速度快，场景需求。

session：会话：建立一次连接
session key：每次会话使用不同的密钥，模仿一次一密。

passwd只做一致性验证，“口令”，不是密码（key），不参与任何变换。

三、Diffie-Hillman密码体制

1.基础知识

本原元：对于一个素数qq，如果数值a(modq)a(mod\quad q),a2(modq)a^2(mod\quad q),…,aq−1(modq)a^{q-1}(mod\quad q)是各不相同的整数,并且以某种排列方式组成了从1到q-1的所有整数，则称整数a是素数q的一个本原元。
离散对数：对于一个整数b和素数q的一个本原元a，可以找到一个唯一的指数i，使得
b≡ai(modq)(0≤i≤q−1)b ≡ a^i(mod\quad q) (0≤i ≤q-1) 成立，则指数i称为b的以a为基数的模q的离散对数。
离散对数难题：已知a和i，求解b是相对容易的，但是已知a和b，求解i是非常困难的。

2.Diffie-Hillman协议

其中大素数q及其原根a是可公开的。

用户A:随机选择一个数xA<qx_A<q，计算yA≡axA(modq)y_A≡a^{x_A}(mod\quad q)。xAx_A作为私钥。yAy_A作为公钥。
用户B:随机选择一个数xB<qx_B<q，计算yB≡axB(modq)y_B≡a^{x_B}(mod\quad q)。xBx_B作为私钥。yBy_B作为公钥。
用户A已知B的公钥yBy_B后，利用自己的私钥计算yBxA=axBxA=axAxB.{y_{B}}^{x_A}={a^{x_B}}^{x_A}={a^{x_A}}^{x_B}.
用户B已知A的公钥yAy_A后，利用自己的私钥计算yAxB=axAxB=axAxB.{y_{A}}^{x_B}={a^{x_A}}^{x_B}={a^{x_A}}^{x_B}.
共享密钥k=axAxBk={a^{x_A}}^{x_B}.

Deffie-Hellman密钥交换算法安全性源于在有限域上计算离散对数，q−12\frac{q-1}{2}应该是一个素数，并且q应该足够大：系统的安全性取决于与q同样长度的数的因子分解的难度；可以选择任何模n的本原元a，通常选择最小的a(一般是一位数)。

q−12\frac{q-1}{2}为什么应该是一个素数？

在 Diffie-Hellman 协议中，我们需要选择一个 q 的生成元 g。生成元 g 的阶是指最小的正整数 n，使得 gn≡1(modq)g^n ≡ 1 (mod\quad q)。由Lagrange定理知，一个群的任意元素的阶都是该群阶的因数。在 DH 协议中，我们关心的是模 q 的乘法群，这个群的阶是 q-1。所以，任意元素（比如生成元 g）的阶必须是 q-1 的因数。因此，如果 (q-1)/2 是素数，那么 q-1 可能因数就只有 1, 2, (q-1) 和 (q-1)/2，所以生成元 g 的阶只可能是这四个数。
因为我们希望生成元 g 的阶尽可能大，以便增加攻击者破解的难度。如果 (q-1)/2 是素数，那么 g 的阶很大可能会是 (q-1) 或者 (q-1)/2，这样就可以提高 DH 协议的安全性。

3.Diffie-Hillman协议的缺陷：中间人攻击

中间人Malice攻击协议，而不是攻击算法。

用户A:随机选择一个数xA<qx_A<q，计算yA≡axA(modq)y_A≡a^{x_A}(mod\quad q)。xAx_A作为私钥。yAy_A作为公钥，发送给M。
用户M:随机选择一个数m<qm<q，计算yM≡am(modq)y_M≡a^{m}(mod\quad q)。发送给B。
用户B:随机选择一个数xB<qx_B<q，计算yB≡axB(modq)y_B≡a^{x_B}(mod\quad q)。xBx_B作为私钥。yBy_B作为公钥，发送给M。
用户M:随机选择一个数m<qm<q，计算yM≡am(modq)y_M≡a^{m}(mod\quad q)。发送给A。

A认为共享密钥是yMxA=amxA=axAm.{y_{M}}^{x_A}={a^{m}}^{x_A}={a^{x_A}}^{m}.
B认为共享密钥是yMxB=amxB=axBm.{y_{M}}^{x_B}={a^{m}}^{x_B}={a^{x_B}}^{m}.
M用A的公钥和自己选的m计算出A所认为的共享密钥。
M用B的公钥和自己选的m计算出B所认为的共享密钥。
从而实现了中间人攻击。

AB之间没有进行任何身份认证机制，所以容易遭受中间人攻击。当A接收到来自M的”公钥“时，并没有认证这个”公钥“来自于B。

四、背包密码体制

背包算法（来自01背包问题）
明文按照物品个数分组，位置一一对齐，给定一系列值m1,m2,…,mnm_1,m_2,…,m_n和一个和ss，计算bib_i使之满足
s=b1m1+b2m2+…+bimi.s = b_1m_1 + b_2m_2 + … + b_im_i.求解很困难，验证很容易。是个NP问题。
∑bimi\sum b_im_i作为密文。b1,b2,...,bnb_1,b_2,...,b_n作为明文。背包序列m1,m2,...,mnm_1,m_2,...,m_n作为公钥。

超递增背包序列：作为私钥，用来解密 。
超递增序列：它的每一项都大于它之前所有项之和；
例一：{1, 3, 6, 13, 27, 52}
超递增背包问题的解：
计算其总重量并与序列中最大的数比较
如果总重量小于这个数，则它不在背包中；
反之，则它在背包中，背包重量减去这个数。
考查数列下一个最大的数，重复直到结束
如果总重量减为零，那么有一个解；
反之无解。
问题的转化
超递增背包问题的解很容易找到；
非超递增背包问题是困难问题，没有快速解法。
超递增背包问题向非超递增背包问题的转化
取一个超递增序列，比如{2, 3, 6, 13, 27, 52}；
分别选取nn和mm，用nn去乘所有的项，mm作为模数进行模运算。比如
n=31,m=105n = 31, m = 105
2×31mod105≡622×31mod105 ≡ 62
⋅⋅⋅\cdot \cdot \cdot
52×31mod105≡3752×31mod105 ≡ 37
得到一个非超递增序列，{62, 93, 81, 88, 102, 37}；
超递增序列作为私人密钥，得到的非超递增序列作为公钥。
其中的盲因子n,m也是不能公开的。

五、RSA密码体制

1.密钥生成、加密、解密

密钥生成
首先选取两个大素数p和q，计算n = pq；（主要时间开销在此，选择大数、判断素性。）
随机选取加密密钥e，使e和(p - 1)(q - 1)互素；（使e在mod(p - 1)(q - 1)下存在逆元）
用扩展欧几里德算法计算解密密钥d，以满足：
e∗d=1mod(p−1)(q−1)e*d = 1mod(p - 1)(q - 1)，即 d=e−1mod(p−1)(q−1)d = e^{-1}mod(p - 1)(q - 1)；
公开钥为(e,n)(e, n)，秘密钥为(d,n)(d, n)。

加密过程
加密的数学变换: C=Me mod nC=M^{e} \bmod n
M>n时，是不方便还原的（一个剩余类）。所以M<n.
如果消息大于M，就分组，加密，再串接。
实际应用多数是加密一些消息密钥和安全参数，常常M<n.

解密过程
解密的数学变换: M=Cd mod nM=C^{d} \bmod n
正确性验证
Cd mod n=(Me)d mod n=Med mod n=Mk(p−1)(q−1)+1 mod nC^{d} \bmod n=\left(M^{e}\right)^{d} \bmod n=M^{e d} \bmod n=M^{k(p-1)(q-1)+1} \bmod n
=M×M(p−1)(q−1) mod n=M \times M^{(p-1)(q-1)} \bmod n (欧拉定理)

M：字符串：看作01代码，再转换成整数

其中的幂运算：（大指数模幂运算：不是先算幂再取模）
快速幂取模
(a×b) mod n≡[(a mod n)×(b mod n)] mod n(a \times b) \bmod n \equiv[(a \bmod n) \times(b \bmod n)] \bmod n

求数m的二进制表达式

带余除法（开销较大）

1
2
3
4
5
6
7
while(m){
int yu=m%2;
a[i]=yu;
m/=2;
i++;
}

----->

1
2
3
4
5
位运算（更快）
while(m){
int temp=m&0x1;
m>>1;
}

RSA的安全性完全依赖于分解大数的难度:
129位十进制数字的模数是能分解的临界数，n应该大于这个数。
RSA的n起初512位，后来提升为1024位（民用）2024位（涉密）。

2.选择密文攻击

加密的公私钥对（公钥加密，私钥解密），不能用来签名（私钥签名，公钥验证）
即不能用同一套密钥加密和签名。

对协议的攻击
例一
Eve在Alice的通信过程中进行窃听，设法成功选取了一个用她的公开密钥加密的密文c。Eve想读出信息m，m=cdm = cd。
Eve选取一个随机数r，满足r小于n。她得到Alice的公钥e：
x≡remodnx ≡ r^e modn
y≡xcmodny ≡ x^c modn
t≡r−1modnt ≡ r^{-1} modn
Eve让Alice用她的私人密钥对y签名，以便解密y：
u≡ydmodnu ≡ y^d modn
Eve计算：
tumodntu \quad modn
≡r−1ydmodn≡ r^{-1} y^d modn
≡r−1xdcdmodn≡ r^{-1} x^d c^d modn
≡cdmodn≡ c^d modn
≡m≡ m

例二
Alice是一个公开的计算机公证人，Eve想让Alice对一个本来不愿意签名的消息签名，例如m1m_1。
如果m1≡m2m3modnm_1≡ m_2m_3 modn
Eve让Alice用她的私人密钥对m2m_2和m3m_3分别签名,从而获得了Alice对m1m_1的签名：
Eve计算：
m1d≡(m2dmodn)(m3dmodn)m_1^d ≡ (m_2^d modn) (m_3^d modn)

同模攻击
对RSA的公共模数攻击
不同的使用者采用相同模数 nn, 即使 ee 和 dd 不同，假如两个公钥互素，则无需任何的解密技术就可以恢复明文。

设 mm 位明文, 两个公钥为 e1e_{1} 和 e2e_{2}, 模数为 nn, 两个密文为:

c1≡me1 mod nc2≡me2 mod nc_{1} \equiv m^{e_{1}} \bmod n \quad c_{2} \equiv m^{e_{2}} \bmod n

由于 e1e_{1} 和 e2e_{2} 互素, 根据扩展欧几里德算法找出 rr 和 ss, 满足:

re1+se2=1r e_{1}+s e_{2}=1

假定 rr 是负数( rr 或 ss 中有一个必须是负数), 用欧几里德算法可计算 c1−1c_{1}{ }^{-1} :

(c1−1)−rc2s=m mod n\left(c_{1}^{-1}\right)^{-r} c_{2}^{s}=m \bmod n

c1rc2s=(me1)r(me2)s=mre1+se2(modn)=m(modn)c^{r}_{1}c^s_{2}=(m^{e_{1}})^r(m^{e2})^s=m^{re_{1}+se_{2}}(mod\quad n)=m(mod\quad n)

六、Elgamal密码体制

该密码体制基于离散对数难题。选择一个素数p，两个随机数g和x(g＜p,x＜p)，计算y≡gxmodpy≡g^xmodp。公开密钥是y、g和p，私钥是x。设待加密消息为m：
加密
首先选择随机数r，只要r与p-1互素；
计算：a≡grmodpa ≡ g^rmodp 和 b≡yrmmodpb ≡ y^rm\quad modp，a和b作为密文对，密文的长度是明文的两倍；
解密
计算： m≡b/axmodpm ≡ b/a^x modp；
验证：ax≡grxmodpa^x≡g^{rx} modp，b/ax≡yrm/ax≡gxrm/gxr≡mmodpb/a^x ≡ y^rm/a^x≡g^{xr}m/g^{xr} ≡ m\quad modp。

七、椭圆曲线密码体制ECC(Elliptic Curve Cryptography)

（注：椭圆曲线是光滑的三次曲线，椭圆是二次曲线，两者不是同一个东西。）

ECC基于椭圆曲线上的离散对数问题。它的求解更难，这使得密钥长度大大减小。
（相同密钥长度，对称加密安全性更强。）

参考：零知识证明 - 椭圆曲线基础 - 知乎 (zhihu.com)

实数域上的椭圆曲线

对于固定的实数a,b，满足方程：y2=x3+ax+b，4a3+27b2(modp)≠0y^{2}=x^{3}+ax+b，4a^3+27b^2(modp) ≠0 的所有点的集合，外加一个零点和无穷远点O，其中x和y是实数域上取值。
有限域GF(2m)GF(2^m)上的椭圆曲线:
其中a,b,x,ya,b,x,y是有限域GF(2m)GF(2^m)上取值。域GF(2m)GF(2^m)上的元素是m位的串。
只要非负整数a和b满足：4a3+27b2(modp)≠04a^3+27b^2(modp) ≠0，那么Ep(a,b)E_{p}(a,b)表示模p的椭圆群，这个群中的元素和一个称为无穷远点的O共同组成椭圆群——Abel群(单位元、逆元、交换律、结合律)。

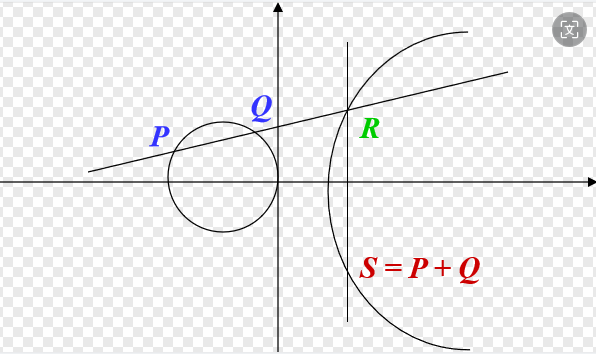
image-20240508221742558
加法规则：
P+Q+R=0P+Q+R=0
P+Q=−R=SP+Q=-R=S
P+PP+P:切线
倍点规则：
P+P+R=2P+R=0P+P+R=2P+R=0
2P=−R=S2P=-R=S
两个互不为逆的点P(x1,y1)和Q(x2,y2)的加法规则
P(x1,y1)+Q(x2,y2)=S(x3,y3)P(x1,y1) + Q(x2,y2) = S(x3,y3)
其中x3=λ2−x1−x2,y3=λ(x1−x3)−y1,λ=(y2−y1)/(x2−x1)x_3=λ^2-x_1-x_2, y_3=λ(x_1-x_3)-y_1, λ=(y_2-y_1)/(x_2-x_1)
对任意点P(x1,y1)的倍点规则
P(x1,y1)+P(x1,y1)=2P(x1,y1)=Q(x3,y3)P(x1,y1)+ P(x1,y1)=2P(x1,y1)=Q(x3,y3)
其中，x3=λ2−2x1,y3=λ(x1−x3)−y1,λ=(3x12+a)/2y1x_3=λ^2-2x_1, y_3=λ(x_1-x_3)-y1, λ=(3x_{1}^2+a)/2y_1
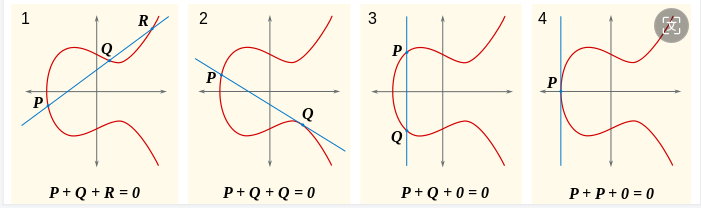
image-20240508221826882

定义一：mP = P + P +…+ P (m个P)
定义二：P是椭圆曲线E上的一个点，若存在最小的正整数n，使得nP = O，其中O是无穷远点，则称n是P的阶数。

加解密过程

系统的建立
选取一个有限域GF(p)和定义在该域上的椭圆曲线E(a,b)和E(a,b)上的一个阶为n的点P(xp, yp)；
GF(p)、a、b、P(xp, yp)和n都是公开信息。
密钥的生成
在区间[1, n-1]中随机选取一个整数d；
计算Q = d×P；
实体的公开密钥是Q，私钥是证书d。
已知d，P，Q易算；已知P,Q，d难算。
消息传输
Bob试图将消息M发送给Alice时，执行下列操作
查找Alice的公钥Q；
将消息M表示成一个域元素m∈GF(p)；
在区间[1, n-1]中随机选取一个整数k；
计算点(x1, y1) = kP；
计算点(x2, y2) = kQ，如果x2 = 0，则返回到第三步；
计算c=mx2c = mx_2；
传送加密数据(x1, y1, c)给Alice。
当Alice解密从Bob收到的密文(x1, y1, c)时，执行下列操作
使用她的私钥d，计算点(x2, y2) = d(x1, y1)；
计算x2−1x_2^{-1}；
计算cx2−1c x_2^{-1}，而cx2−1=mx2x2−1=mc x_2^{-1} = mx_2 x_2^{-1} = m，即恢复出明文。

整数到域元素的转换
文字消息—ascii----二进制01串----整数-----域元素
平方剩余
如果p是素数，且a小于p，如果 x2 ≡ a modp对于一些x成立，则称a是对模p的平方剩余。
例如：p = 7, 4 ≡ 22 ≡ 52 mod7 (2和5称为平方根)
整数到域元素的转换(设明文消息是m, 0≤m≤M)
取一个足够大的整数k∈[30,50]；
不妨取k = 30，计算一系列的x∈{mk+j}j =0,1,2…，直到x3+ax+b(modp)是模p的平方剩余；
(x, (x3+ax+b)1/2)即为椭圆曲线上的点。

八、针对协议的劫持攻击

image-20240510114033024